指数・対数関数の基本
(1)累乗の基本
1.累乗の定義
a が実数で n が整数の時,an = a × a × ・・・ × a (a を n 回掛ける)と書き表す。これを a の n 乗と呼び,このような演算のことを累乗と呼ぶ。
(例)38 = 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 = 6561
2.累乗の法則
累乗の性質から考えて,以下のことが成り立つことは分かるであろう。
- a が実数,m・n が正整数の時 am × an = am + n
- a が実数,m・n が正整数の時 (am)n = am × n
- a・b が実数,m が正整数の時 am × bm = (a × b)m
実例を挙げてみると
- 35 × 33
= (3 × 3 × 3 × 3 × 3) × (3 × 3 × 3)
= 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3
= 38
= 35 + 3 - (33)2
= (3 × 3 × 3)2
= (3 × 3 × 3) × (3 × 3 × 3)
= 3 × 3 × 3 × 3 × 3 × 3
= 36
= 33 × 2 - 24 × 54
= (2 × 2 × 2 × 2) × (5 × 5 × 5 × 5)
= (2 × 5) × (2 × 5) × (2 × 5) × (2 × 5)
= (2 × 5)4
(2)実数の累乗と指数関数
1.ゼロの累乗
ここで,a0というものを考えてみる。
上の法則が正整数だけでなく0でも成り立つと考えると,公式1より(n は正整数)
an × a0 = an + 0 = an
∴ an × a0 = an
a ≠ 0 であれば,この両辺を anで割って a0 = 1 が得られる。a = 0 のときは 00 は定まらないため考えないものとする。
「a ≠ 0 である任意の実数 a について,a0 = 1 が成り立つ」と定義する。
2.負の整数の累乗
さらに,a-n(n は正整数)というものを考えてみる。
上の法則が0以上の整数だけでなく負の整数でも成り立つと考えると,公式1より(a は0でない実数)
an × a-n = an + (-n) = a0 = 1
∴ an × a-n = 1
a ≠ 0 であるから,この両辺を anで割って
| a-n = | 1 |
| an |
が得られる。
「a ≠ 0 である任意の実数 a について,a-n = 1/an が成り立つ」と定義する。
3.有理数(分数)の累乗
さらに,am/n(m,n は整数)というものを考えてみる。
上の法則が有理数でも成り立つと考えると,公式2より(a は0でない実数)
(am/n)n = a(m/n) × n = am
∴ (am/n)n = am
すなわち,am/n の n 乗が am なのでである。
一般に,実数 x に対して x を n 乗すると y になるとき(n は正整数),y を「x の n 乗根」と呼ぶ。
特に2乗根は「平方根」(ABではSqr関数として利用可能),3乗根は「立方根」と呼ぶ。
(例1)9の2乗根(平方根)は「√9」と書き表す。9 = 32 であるから √9 = 3 である。
(例2)16の4乗根は「4√16」と書き表す。16 = 24 であるから 4√16 = 2 である。
(例3)一般に累乗根はきっちりとした数字に収まるとは限らない。例えば √2 = 1.41421356237 ... と無限小数になる。
【注意】
奇数乗根はどんな実数にも存在するが,偶数乗根は0以上の実数にしか存在しない(なぜなら,正の数でも負の数でも2乗すれば正になるため)。
また,正の数に対する偶数乗根は2つ存在する(例えば,22 = (-2)2 = 4 なので 2 と -2 は 4 の平方根)。ただし特に断りなく「n√a」(n は偶数)と書いた場合は,累乗根のうち正のもののみを指すこととする(例1〜3もこれに従っている)。
結局,「a ≠ 0 である任意の実数 a について,am/n = n√am が成り立つ」と定義できる。
ただし,aが負の実数であればnは奇数に限定される。
4.実数の累乗
このように考えていくと,実数全体に対して累乗が考えられそうな気がしてきただろう。現在のところ有理数しか考えていないが,実際には無理数(2整数の商として表せない数。π(円周率)などがこれにあたる)にも「有理数の間を縫う」ようにすれば,正の数に対しては「無理数で累乗する」という演算が定義できる(厳密な証明は大学レベルになるので略)。
5.指数関数
a を正の数(定数),x を実数(変数)として y = ax のような関数を考える。これを指数関数という。もし a = 1 であれば常に y = 1 であるので,ここでは a ≠ 1 の場合のみを考える。
a > 1 の場合,グラフはおおよそ次のような形になる。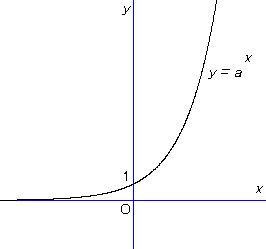
a < 1 の場合,グラフはおおよそ次のような形になる。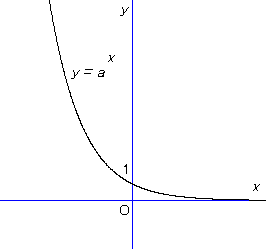
(3)対数
1.対数
y = ax の関係が成立する時,y から x を見た式を考える(すなわち,x = f(y) の形に表す)。
y = ax を x を見た式として x = logay という表記を定義する。logay というのは,「a を何乗すると y になるか」を表している。これを「対数」という。
もとの指数関数の意味より,上の式においてyは正の数に限られ,a(これを「
2.対数の性質
対数は以下の性質を満たす。
- x・yが正の数,a が1でない正の数のとき loga(x × y) = logax + logay
- x・yが正の数,a が1でない正の数のとき loga(x ÷ y) = logax - logay
- xが正の数,pが実数,a が1でない正の数のとき loga(xp) = p × logax
- xが正の数,a・b が1でない正の数のとき logax = logbx ÷ logba
3.対数関数
a を1でない正の数(定数),x を正の数(変数)として y = logax のような関数を考える。これを対数関数という。
対数の定義より,対数関数のグラフは指数関数のグラフのx軸とy軸を入れ替えた状態になる。
a > 1 の場合,グラフはおおよそ次のような形になる。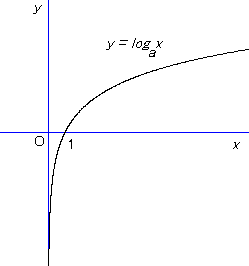
a < 1 の場合,グラフはおおよそ次のような形になる。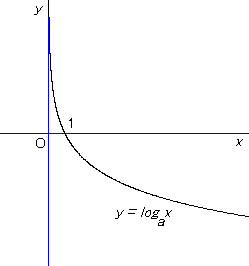
4.対数関数の微分
対数関数を微分する(詳細略)と,以下のようになる。
(logax)' = 1 / (x × logea)
ここで e は (1 + t)1 / t → e (t → 0) となる定数である。
そこで,逆に「導関数が 1 / x となるような対数」を考え,これを自然対数と言う。
自然対数は定義の通り logex のように表されるが,単にその意味で「log x」と書くこともある。またたまに「ln x」と書かれることもある('ln' = 'natural logarithm':「自然対数」)。
通常,プログラミング言語での対数関数(BASICでは Log 関数)は自然対数である。これはコンピュータ上での計算がしやすいためである。別の底の対数関数を計算するには,「対数の性質」の4を使えばよい。
(例)BASICで log102 を計算する場合,log102 = loge2 ÷ loge10 だから,計算式は Log(2)/Log(10) とすればよい。
また,eを底にした指数関数には微分について以下のような性質がある。
(ex)' = ex
(補注:(ax)' = ax × logea
つまり,eを底にした指数関数は微分すると元の関数に戻る。なおBASICの Exp 関数は ex を計算する関数である。