三角関数の基本

三角関数とは

三角関数は，以下のように定義されている。

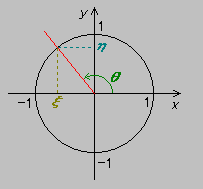平面上の座標において，x軸上の正の部分を始点として左回りに角度θを取り，原点からその角度に半直線を引く（図の赤い直線の部分）。この直線と，原点を中心とした半径１の円との交点のx座標をξ，y座標をηとすると，sin θ・cos θ・tan θは以下のようになる。

sin θ = η
cos θ = ξ
tan θ = η / ξ

また，上の図から以下のことがわかる。

sin θ / cos θ = tan θ
sin² θ + cos² θ = 1 （三平方の定理を用いる）

注 (sin θ)² をよく sin² θ と記述する（他も同様）。

ラジアン

通常プログラミング言語において，三角関数の引数はラジアン（rad）を用いる。1ラジアンは(180/π)度に等しい。

主な角度の「度」と「ラジアン」の対応表

度	ラジアン
0	0
1	(1/180)×π
15	(1/12)×π
30	(1/6)×π
45	(1/4)×π
180/π (≒ 57.2958)	1

度	ラジアン
60	(1/3)×π
90	(1/2)×π
135	(3/4)×π
180	π
270	(3/2)×π
360	2π

ラジアンを用いた三角関数の値は，無限数列を用いて求められる。この無限数列の計算をコンピュータ内部で行うことで三角関数は求められている。
ActiveBasicの「Include\basic\function.sbp」の中の「_Support_tan」関数を見ると，「For i=19 To 3 Step -2」という部分があるが，ここがそれに相当している（多分）。

余談だが，ラジアンを使うと三角関数の微分・積分も可能になる。

(sin x)' = cos x
(cos x)' = -sin x
(tan x)' = tan² x + 1

応用

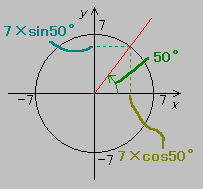
（例）x-y座標^※において，50度の方向^※を向いている時に長さ7だけ前進した。移動後のx座標，y座標の値はいくらか。
※座標および角度は，このページの一番上で定義したものの通りとする。

（答）右の図のように計算できる。

x座標：7 × cos 50°≒ 7 × 0.6428 ≒ 4.4996
y座標：7 × sin 50°≒ 7 × 0.7660 ≒ 5.3620

注：sin および cos の値は，Windowsの電卓を用いて出しました。

アークタンジェント

y = tan x （x はラジアン，-2/π ≦ x ≦ 2/π）のとき，x = Tan^-1 y と書き（「-1」は「-1乗」ではなくただの記号としてみて下さい），x を y のアークタンジェントと呼ぶ。アークサイン・アークコサインも，x の範囲をそれぞれ -2/π ≦ x ≦ 2/π，0 ≦ x ≦ π に取れば同様に定義される。
アークタンジェントは，よく円周率の値を求めるのに用いられる。tan 45° = tan(π/4) = 1 であるから，π = 4 Tan^-1 1 となる。

BASICでは，アークタンジェントは Atn と書かれる（Cなんかではatanと書く）。ActiveBasicの場合，アークサイン・アークコサインは標準では計算できず，以下の方法を用いる。

Sin^-1 x = Tan^-1(x/√1 - x²)
Cos^-1 x = Tan^-1(√1 - x²/x)

戻る